“熵”

热统系列之5

自信息熵、条件熵、联合熵、互信息

香农根据概率取对数后的平均值定义信息熵。如果只有一个随机变量，比如一个信息源，定义的是源的自信息熵。如果有多个随机变量，可以定义它们的条件概率、联合概率等，相对应地，也就有了条件熵、联合熵、互信息等等，它们之间的关系如下面左图所示。

图1：条件熵、联合熵、和互信息

比如说，最简单的情况，只有两个随机变量X和Y。如果它们互相独立的话，那就只是将它们看成两个互相不影响的随机变量而已，在那种情形，上面图1左图中的两个圆圈没有交集，变量X和Y分别有自己的自信息熵H(X)和H(Y)。如果两个变量互相关联，则两个圆圈交叉的情况可以描述关联程度的多少。图1中的条件熵H(X|Y)表示的是，在给定随机变量Y的条件下X的平均信息量；相类似地，条件熵H(Y|X)是随机变量X被给定的条件下Y的平均信息量。联合熵H(X,Y)，则是两个变量X,Y同时出现（比如同时丢硬币和骰子）的信息熵，也就是描述这一对随机变量同时发生平均所需要的信息量。图1中两个圆的交叉部分I(X;Y)被称为互信息，是两个变量互相依赖程度的量度，或者可看作是两个随机变量共享的信息量。

信息论中的熵通常用大写字母H表示，如图中的H(X)、H(Y)、H(X|Y)、H (Y|X)等，但互信息通常被表示为I(X;Y)，不用字母H。其原因是因为它不是直接从概率函数的平均值所导出，而是首先被表示为“概率比值”的平均值。从图1右边的公式可见，联合熵是联合概率的平均值，条件熵是条件概率的平均值，互信息则是“联合概率除以两个边缘概率”的平均值。

直观地说，熵是随机变量不确定度的量度，条件熵 H(X|Y)是给定Y之后X的剩余不确定度的量度。联合熵是X和Y一起出现时不确定度的量度。互信息I(X;Y)是给定Y之后X不确定性减少的程度。

互信息的概念在信息论中占有核心的地位，可以用于衡量信道的传输能力。

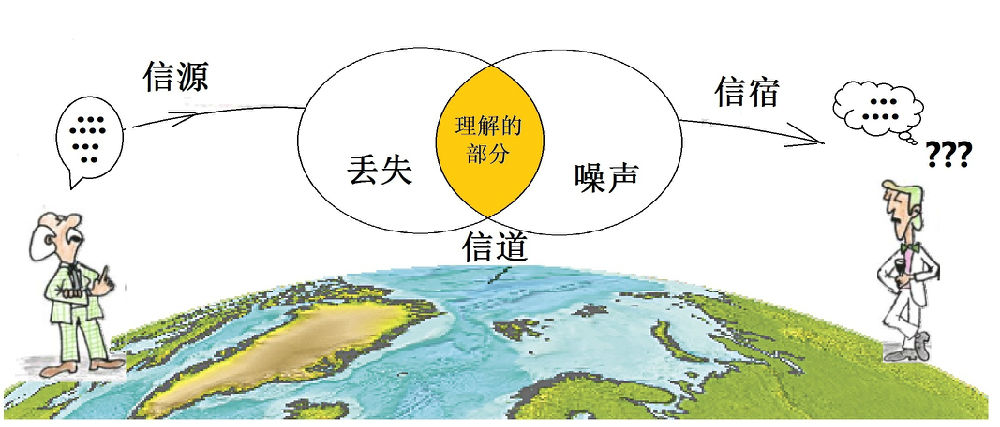
图2：信息传输过程中的互信息

如图2所示，信源（左）发出的信息通过信道（中）传给信宿（右）。信源发出的信号，和信宿收到的信号，是两个不同的随机变量，分别记作X和Y。信宿收到的Y与信源发出的X之间的关系不外乎两种可能：独立或相关。如果Y和X独立，说明由于信道中外界因素的干扰而造成信息完全损失了，这时候的互信息I(X;Y)=0，通信中最糟糕的情况。如果互信息I(X;Y)不等于0，如图中所示的橘色重叠部分，表明不确定性减少了。图中两个圆重叠部分越大，互信息越大，信息丢失得越少。如果Y和X完全相互依赖，它们的互信息最大，等于它们各自的自信息熵。

互信息在本质上也是一种熵，可以表示为两个随机变量X 和 Y相对于它们的联合熵的相对熵。相对熵又被称为互熵、交叉熵、KL散度、等。

首先，对一个随机变量X，如果有两个概率函数p(x), q(x)，相对熵被定义为：

在互信息的情形，如图1右下方的I(X;Y) 表达式，被两个随机变量X和Y定义，也可看成是相对熵，在一定程度上，可以看成是两个随机变量距离的度量。

两个随机变量的互信息不同于概率论中常用的相关系数（correlation）。相关系数表示两个随机变量的线性依赖关系，而互信息描述一般的依赖关系。相关系数一般只用于数值变量，互信息可用于更广泛的包括以符号表示的随机变量。

最大熵原理

热力学和统计物理中有热力学第二定律，即熵增加原理，信息论中则有最大熵原理。

我们在日常生活中经常碰到随机变量，也就是说，结果不确定的事件。诸如旋转硬币掷骰子，都是例子。还有比如说，球队A要与球队B进行一场球赛，结果或输或赢；明天的天气，或晴或雨或多云；股市中15个大公司的股价，半年后有可能是某个范围之内的任何数值……但是，在大多数情况下，人们并不知道随机变量的概率分布，或者说，只知道某个未知事件的部分知识而非全部，有时候往往需要根据这些片面的已知条件来猜测事件发生的概率。有时猜得准，有时猜不准，猜不准损失一点点，猜准了可能赚大钱。事件发生的随机性及不可知性，就是支持赌城的机器不停运转的赌徒心态的根源。

人们猜测事件发生的概率，多少带有一定的主观性，每个人有他自己的一套思维方法。如果是一个“正规理性”（这个概念当然很含糊，但假设大多数人属于此类）思维的人，肯定首先要充分利用所有已知的条件。比如说，如果小王知道球队A在过去与其他队的10场比赛中只赢过3次，而球队B的10场比赛赢过5次的话，他就应该将赌注下到球队B上。但是，小李可能了解了更多的消息：球队B的主要得力干将上个月跳槽到球队A来了，所以，他猜这次比赛球队A赢的可能性更大。

除了尽量利用已知信息外，还有没有什么其它客观一点的规律可循呢？也就是说，对于随机事件中的未知部分，人们“会”如何猜测？人们“应该”如何猜测？举例说，小王准备花一笔钱投资来买15个大公司的股票，如果他对这些公司一无所知，他选择的投资方案很可能是15种股票均分。如果有位行家告诉他，其中B公司最具潜力，其次是G公司。那么，他可能将更多的钱投资到B和G，其余的再均分到剩下的13种股票中。

上面的例子基本符合人们的常识，科学家却认识到这其中可能隐藏着某种大自然的玄机。大自然最玄妙的规律之一是最小作用量原理，造物主喜欢极值，或者说凡事讲究最优化。统计规律中的随机变量也可能遵循某种极值规律。

如上所述，随机变量的信息熵与变量的概率分布曲线对应。那么，随机变量遵循的极值规律也许与熵有关！信息熵来自于热力学熵，信息熵的“不确定程度的度量”也可以用来解释热力学熵。当然，热力学中（物理中）不确定性的来源有多种多样，必须一个一个具体分析。经典牛顿力学是确定的，但是，我们无法知道微观粒子的情况，这点带来了不确定性。也许是因为测量技术使我们无法跟踪，也许是因为粒子数太多而无法跟踪，也有可能是我们主观上懒得跟踪、不屑于跟踪，反正就是不跟踪，即“不确定”！如果考虑量子力学，还有不确定原理，那种非隐变量式的，爱因斯坦反对的本质上的不确定。即使是牛顿力学，也有因为初始条件的细微偏差而造成的“混沌现象”，蝴蝶效应式的不确定。此外，还有一种因为数学上对无穷概念的理解而产生的不确定。

总之，物理中的熵也能被理解为对不确定性的度量，物理中有熵增加原理，一切孤立物理系统的时间演化总是趋向于熵值最大，朝着最混乱的方向发展。那么，熵增加原理是否意味着最混乱的状态是客观事物最可能出现的状态？从信息论的角度看，熵最大意味着什么呢？1957年，美国圣路易斯华盛顿大学的物理学家E.T.Jaynes研究该问题并提出信息熵的最大熵原理，其主要思想可以用于解决上述例子中对随机变量概率的猜测：如果我们只掌握关于分布的部分知识，应该选取符合这些知识但熵值最大的概率分布。因为符合已知条件的概率分布一般有好些个。熵最大的那一个是我们可以作出的最随机，也是最符合客观情况的一种选择。Jaynes从数学上证明了：对随机事件的所有预测中，熵最大的预测出现的概率占绝对优势。

接下来的问题是：什么样的分布熵值最大？对完全未知的离散变量而言，等概率事件（均衡分布）的熵最大。这就是小王选择均分投资15种股票的原因，“不要把鸡蛋放到一个篮子里”，不偏不倚地每种股票都买一点，这样才能保留全部的不确定性，将风险降到最小。

如果不是对某随机事件完全无知的话，可以将已知的因素作为约束条件，同样可以使用最大熵原理得到合适的概率分布，用数学模型来描述就是求解约束条件下的极值问题。问题的解当然与约束条件有关。数学家们（Tribus等）从一些常见的约束条件得到几个统计学中著名的典型分布，如高斯分布、伽马分布、指数分布等，这些自然界中常见分布，实际上都是最大熵原理的特殊情况。 最大熵理论再一次说明了造物主的“智慧”，也见证了“熵”这个物理量的威力！

马尔可夫链

到此为止，我们的讨论基本是针对随机变量而言。如果有一连串的随机变量按时间排列起来，就叫做随机过程。实际上，就广义而言，这儿的“过程”不一定仅仅代表“时间”序列，反正是一个序列就行，特别是对离散的、信息论中感兴趣的那些序列，比如文字这种东西，一个接一个，未必见得需要理解成时间。

本文的开头介绍过因多个（主要是两个）随机变量之间的关联情况而定义的“熵”。当我们考虑一连串的随机变量时，这些变量之间有可能互相关联。最简单的情况是下一个状态的条件概率分布仅仅只依赖于当前的状态，这种性质叫做“无记忆”的马尔可夫性质，因安德烈・马尔可夫（A.A.Markov，1856－1922）得名，如果是离散变量组成的具有马尔可夫性质的一连串随机变量，则被称为马尔可夫链。

在马尔可夫链的每一步，系统根据概率分布，从一个状态变到另一个状态。比如说，下图a所示表明某一天的天气转换到下一天天气的概率。

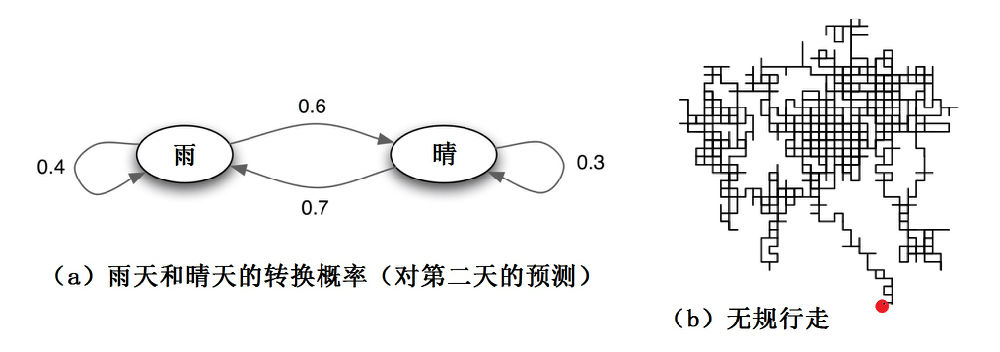
图3：马尔可夫链举例

这儿的所谓天气，只简单地用两个变量：雨或晴来表示。你每天早上8点醒来，便观察天气是“雨”或者“晴”，如果每天8点钟“雨晴”的变换规律是一个马尔可夫链，并简单地符合图3a给出的“雨晴”概率转换图（或可表示成一个2x2的矩阵），你可以从当天的状态，推测第二天“雨或晴”的概率。

随机漫步（布朗运动模型之一）是马尔可夫链的另一个典型例子。最简单的二维随机漫步（图3b）中的每一步，可以移动到任何一个相邻的格点（这儿的变量数比“天气”例子中多了一点，有东南西北四个方向），且移动到每一个点的概率都是相同的，无论之前漫步路径如何，下一个点的位置只与当前这一个点的位置有关，然后依次类推。

Kolmogorov 熵

Kolmogorov熵（K）是系统混沌性质的一种度量，它与Lyapunov 指数之间存在一定的关系。Kolmogorov熵是常用的表征系统混沌性质的熵中的一种，是描述动力学系统轨道分裂数目渐进增长率的度量。动力学系统按其混沌程度可分为规则、确定性混沌和随机。对于规则运动，K=0；在完全随机运动中，K→∞；若系统表现为确定性混沌运动，则K是一个大于零的常数。因此，Kolmogorov熵越大，系统的混沌程度越大，或者说动力系统越复杂。

拓熵(Topological Entropy)

Kolmogorov 熵在拓扑空间中的相似定义。描述连续映射的不确定性。

上两个“熵”与混沌有关，但已经不属于信息论范围，就此打住。